Project 1: Manual neural control

For control problems, spiking models such as the LIF model, are surprisingly useful. We can interpret the firing/non-firing of the neuron as a means to turn on and off a signal. On when the neuron is firing (1). Off when the neuron is silent (0).

Spiking neural systems are useful for control systems because we can exploit the temporal dynamics to react to stimulus in the environment. On this page, we use the leaky integrator (LI) and leaky integrate-and-fire (LIF) models to solve simple problems with very few neurons.

Using spiking neurons for control

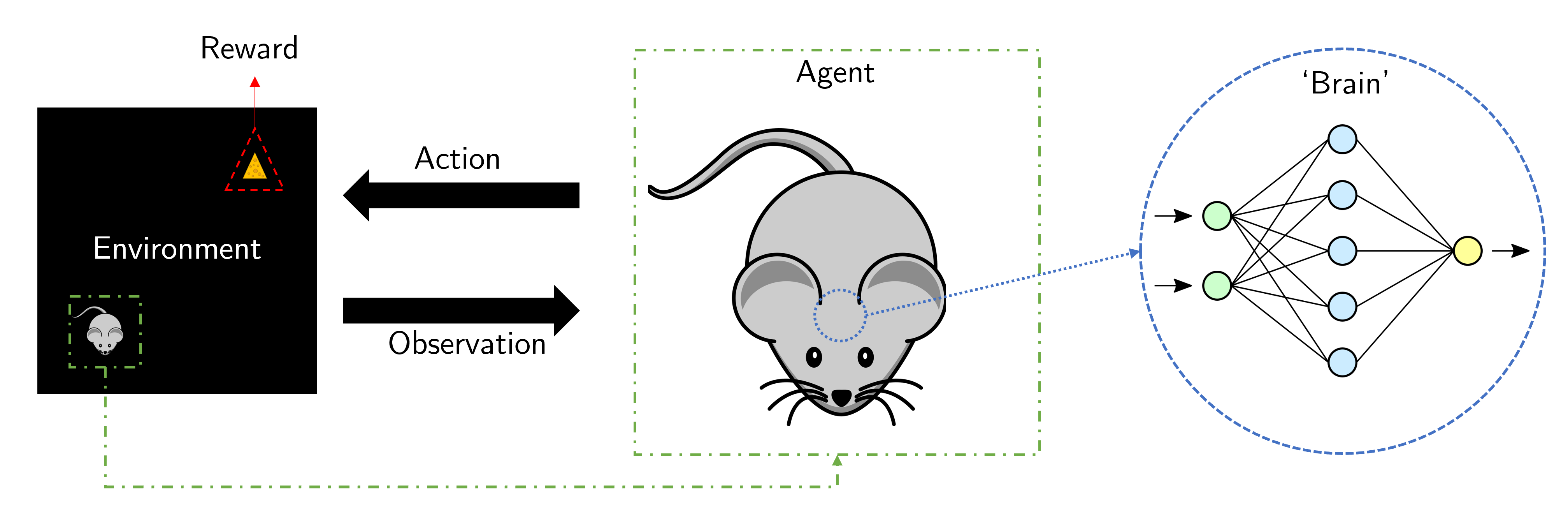
Fig. 4 A closed control loop where an agent, controlled by a neural network, acts upon an environment that responds with observations (such as rewards, like cheese).

Consider the following scenario: a mouse is walking around an environment looking for food. There is now a feedback loop between the mouse (agent) that 1) receives sensory observations, it can then 2) mull over in its artificial brain, so that it 3) can act upon the environment - probably with the hopes of fetching cheese.

Zooming in on the brain, we can imagine the sensory signal (say, distance to cheese) can translate quite directly to a motor output: if the cheese if far away, go faster. Otherwise, stop and enjoy the cheese. If we have one neuron encoding for distance, then we have a small network that could look like this:

    Distance  --->  Leaky integrator  --->  Motor neuron

Referring to the leaky-integrator above in Fig. 1, we can inject a specific current into our leaky integrator and get:

    0.1       --->  Leaky integrator  --->  0.5

Of course, 0.5 may be too much or too little, so it would be desirable to scale it with some factor. For that, we have weights:

    0.1       --->  Leaky integrator  --->  0.5  --->  Multiply by 2  --->  1.0

This is probably starting to look familiar to you because it closely resembles neural networks. And we can literally code this with a few lines of Python using Norse.

import norse.torch as norse

neuron = norse.LIBoxCell()
voltage, state = neuron(0.5)
scaled_output = voltage * 2

Note that the code above is identical to the diagram we drew before: we create a leaky integrator (LIBoxCell), apply a certain current, and scale it by a factor of 2.

The above building blocks are sufficient to understand what happens in our tasks because the situation is the same:

1. We provide input to n neurons that each code for some signal (like distance to food)

2. We read the neuron response output (like neuron voltage or spike)

3. (Optional) We may repeat step 1-2 with additional layers of neurons

4. We provide the neuron output to the environment and repeat

Project tasks

We will be working with two different settings, resulting in three different neurorobotics tasks!

To get started with each task, click on the links below.

Task	Description	Link
1. Cartpole	Balance a wobbly cartpole	Click to start the experiment
2. Mice and cheese	Help a mouse find cheese	Click to start the experiment
3. Mice and mazes	Help a mouse find cheese, with obstacles!	Click to start the experiment